sqrt

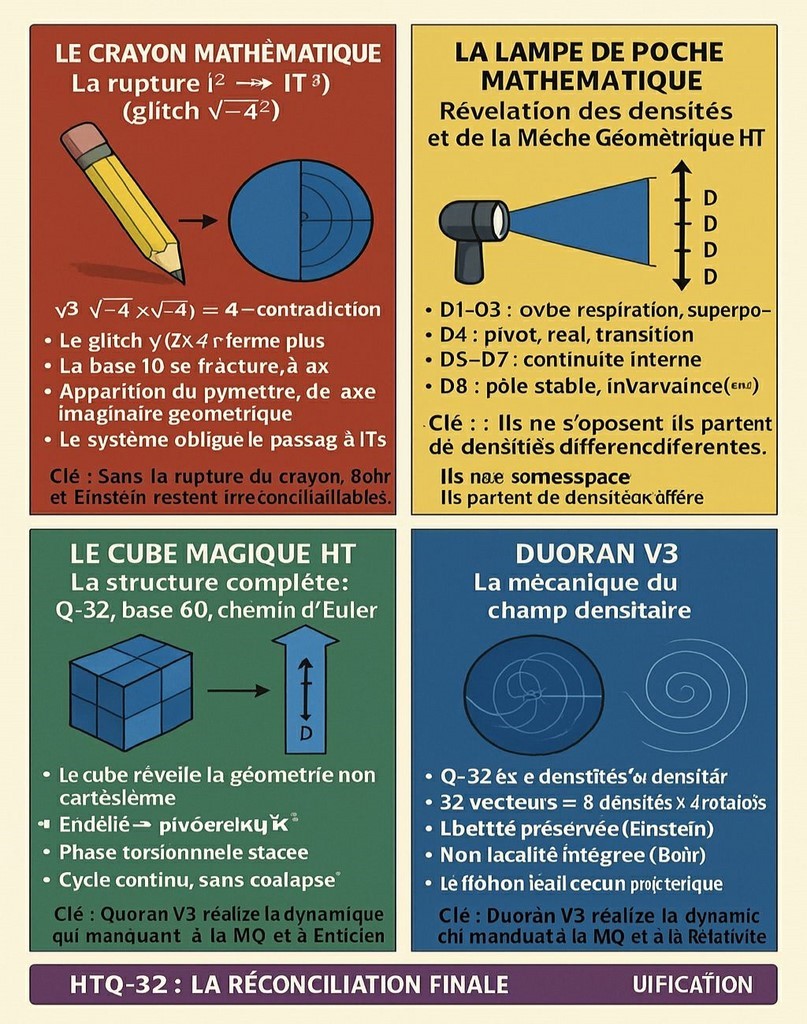
[🔥] √(–4) × √(–4)  (Einstein VS Bohr)
Bohr was right — and Einstein was right as well. They were not contradicting each other : they were looking at two different roads of the same equation.
In HT terms : √(–4) × √(–4) has two solutions, two paths :
7 (the geometric road, Bohr’s intuition) and –4 (the algebraic road, Einstein’s intuition).

Bohr saw the geometry of states. Einstein saw the algebra of reality. Both were correct — they were just standing on two conjugate branches of the same structure. With the HT formalism (Euler road / IT³), these two roads finally reunite. The old argument between “quantum geometry” and “local realism” dissolves : intrication and ordre coexist, as two faces of the same vectorial root.

The disagreement between Bohr and Einstein was never a contradiction.
It was the consequence of a deeper mathematical duality.

HT formalism shows that : √(–4) × √(–4) has two legitimate solutions:
7 → geometric branch (Bohr’s intuition : quantum geometry of states)
–4 → algebraic branch (Einstein’s intuition : deterministic structure)
The two physicists were exploring two complementary roads of the same equation. HT (via Euler paths and IT³ geometry) demonstrates how these branches coexist within a single vectorial root.

This reinterpretation resolves the apparent tension between locality and entanglement, restoring coherence to both visions.

[🔥] √(–4) × √(–4) (Einstein VS Bohr) : Bohr avait raison — et Einstein avait raison aussi. Ils ne se contredisaient pas : ils regardaient deux routes différentes d’une même équation. En termes HT : √(–4) × √(–4) possède deux solutions, deux chemins : 7 (la route géométrique, l’intuition de Bohr) et –4 (la route algébrique, l’intuition d’Einstein). Bohr voyait la géométrie des états. Einstein voyait l’algèbre du réel. Les deux avaient raison — ils se tenaient simplement sur deux branches conjuguées d’une même structure. Avec le formalisme HT (chemin d’Euler / IT³), ces deux routes se rejoignent enfin.
Le vieux débat entre « géométrie quantique » et « réalisme local » se dissout : intrication et ordre coexistent, comme les deux faces d’une même racine vectorielle. Le désaccord entre Bohr et Einstein n’a jamais été une contradiction. Il provenait d’une dualité mathématique plus profonde. 

Le formalisme HT montre que :
 √(–4) × √(–4) possède deux solutions légitimes :
7 → branche géométrique (intuition de Bohr : géométrie quantique des états)
–4 → branche algébrique (intuition d’Einstein : structure déterministe)

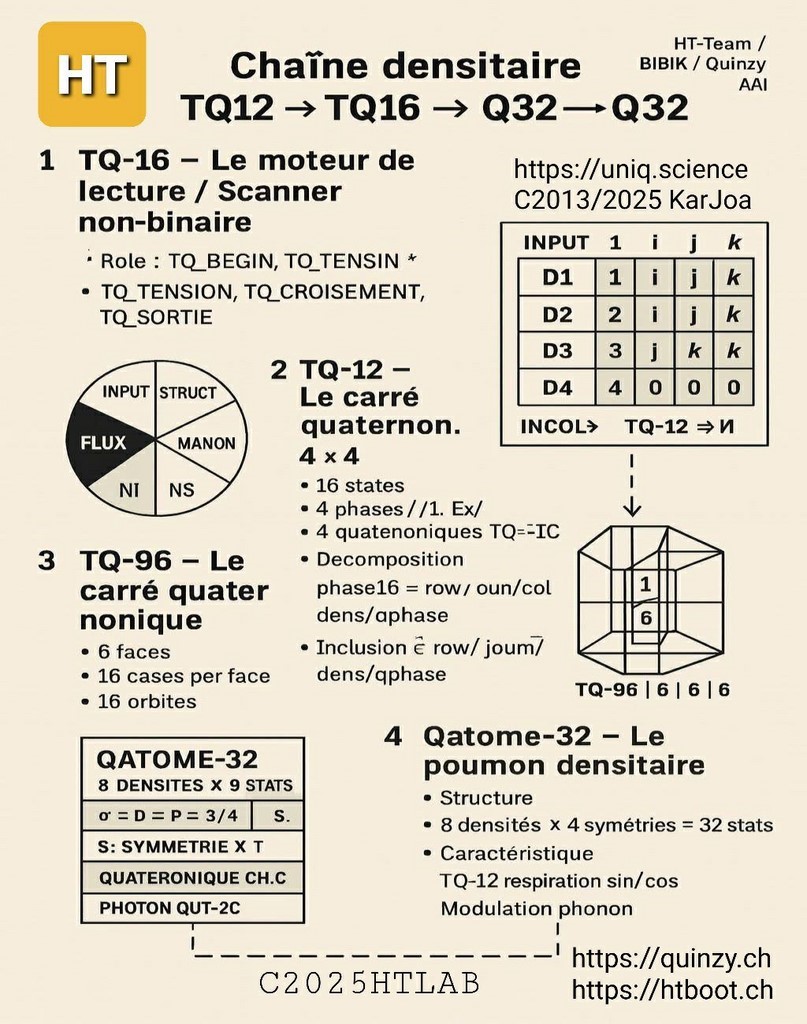
Les deux physiciens exploraient deux routes complémentaires d’une même équation. HT (via les chemins d’Euler et la géométrie IT³) démontre comment ces branches coexistent dans une racine vectorielle unique. Cette réinterprétation résout la tension apparente entre localité et intrication, et rend cohérentes les deux visions. C(2013/2025) HTLAB - KarJoa - https://uniq.science - université des sciences quantiques - 202512010921

Deux chemins pour le cube en "CheckSomme" - un chemin pour algébrique de Euler avec -4 et un chemin logique géométrique avec 7 - Einstein et Bohr , deux facette de la même réalité